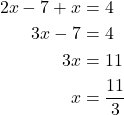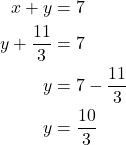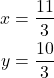Tag Archives: online tutor Pakistan

Online GED Tutor Pakistan

September 8, 2020GED Test, Online Tuition Pakistan, Online Tuition Saudi Arabia, Online Tutor Pakistan, Online Tutor Saudi Arabia, Pakistani TutorsEligibility requirement of GED, FAQ about GED, GED Center Karachi, GED in Karachi, GED in Lahore, GED in Pakistan, GED math Tutor Karachi, GED Pakistan, GED Test Center, GED Test Preparation, GED Testing Service in Pakistan, GED tutoring Center in Islamabad, GED Tutoring Center in Karachi, GED Tutoring in Karachi, Online Tuition Pakistan, Online Tuition Saudi Arabia, online tutor, online tutor Pakistan, SAT 1, SAT 2, SAT online tutor Pakistan, SAT Tutor Pakistan, Universities accept GED in Pakistan, what GED test is?, Who can take GEDalsaudia

Online GED Tutor Pakistan

Welcome to ASVA, Pakistan’s most trusted online tutor academy, offering top-notch GED tuition services. Our expert tutors provide comprehensive GED exam preparation, ensuring that you excel in your exams.

GED Tutors in Pakistan:

Comprehensive Online Tuition for GED Test Preparation

If you’re looking for GED tutors in Pakistan, look no further. Our online tuition services in Pakistan, specifically in Karachi, provide comprehensive preparation for the GED test. We understand the importance of achieving a GED certification, and our experienced tutors are here to guide you every step of the way. With our proven track record of success, we commit to helping you succeed in your GED journey.

I.B.A. Test Preparation

M.B.A. Test Preparation and Expert Entry Test Tutors in Karachi In addition to GED test preparation, we offer specialized assistance for various other tests, including M.B.A. tests, Karachi University exams, I.B.A., LUMPS, and other universities in Pakistan.

Our expert entry test tutors know the requirements of these exams well and offer targeted guidance to help you excel. Whether you need assistance with GRE, GMAT, M.B.A., GED, SAT, IELTS, or TOEFL, our tutors can support you in achieving your goals.

Entry Test Preparation in Saudi Arabia

Online Comprehensive Entry Test Preparation in Saudi Arabia We are proud to extend our online comprehensive entry test preparation services to students in Saudi Arabia as well. With the convenience of online learning, students in Saudi Arabia can access our expert tutors from the comfort of their homes. We understand the unique requirements of entry tests and tailor our instruction to ensure that we fully prepare you to tackle the challenges of these exams.

Entry Test Tutors in Karachi

Best Online Entry Test Tutors in Karachi and Expert IELTS Tutors When it comes to online entry test preparation, we take pride in being the best in Karachi. Our tutors are highly qualified and experienced, specializing in various fields such as engineering, medical sciences, business studies, and more. Additionally, Our dedicated expert IELTS tutors provide help to ensure you achieve your desired score. With their guidance, you can enhance your English language skills and excel in the IELTS exam.

FAQs about GED Test

Q: What is the GED test?

A: The General Educational Development (GED) test is a set of exams designed to assess the knowledge and skills equivalent to those of a high school graduate. It provides an opportunity for individuals who did not complete high school to earn a credential that is widely recognized as an equivalent to a high school diploma.

Q: What subjects are covered in the GED test?

A: The GED test covers four subjects:

Reasoning Through Language Arts (RLA): This section tests reading comprehension, grammar, and writing skills.
Mathematical Reasoning: This section assesses mathematical concepts and problem-solving skills.
Social Studies: This section covers topics such as history, geography, civics, and economics.
Science: This section focuses on scientific reasoning and knowledge in areas such as life sciences, physical sciences, and Earth and space sciences.

Q: How long does it take to complete the GED test?

A: The GED test is divided into separate sections, and the total test duration varies. Typically, the entire test can take around 7.5 hours to complete. However, test-takers can choose to take each subject test separately, allowing for more flexibility in scheduling.

Q: What is the passing score for the GED test?

A: Each subject test in the GED is scored on a scale from 100 to 200. To pass, you need a minimum score of 145 on each subject test. Achieving a score of 165 or higher on a subject test can qualify you for the GED College Ready level, which indicates readiness for college-level courses.

Q: How can I prepare for the GED test?

A: There are various ways to prepare for the GED test:

Self-Study: You can use GED preparation books, online resources, and practice tests to study independently.
GED Classes: Many community colleges and adult education centers offer GED preparation classes.
Online Resources: Several websites provide study materials, practice tests, and interactive lessons specifically tailored for the GED test.
GED Test Prep Courses: There are commercial GED test prep courses available that offer structured instruction and support.

Q: Where can I take the GED test?

A: The GED test is administered at official GED testing centers, which can be found in various locations, such as community colleges, adult education centers, and testing centers. You can find a nearby testing center by visiting the official GED website or contacting your local adult education office.

Q: Can I take the GED test online?

A: Yes, in response to the COVID-19 pandemic, some locations have offered online GED testing options. However, availability and eligibility for online testing may vary depending on your location and specific circumstances. It’s best to check with the official GED website or your local GED testing center for the most up-to-date information.

Q: Is the GED test accepted by colleges and employers?

A: Yes, the GED credential is widely accepted by colleges, universities, and employers as equivalent to a high school diploma. However, it’s always recommended to check with specific institutions or employers to ensure they recognize the GED credential.

Q: Can I retake the GED test if I don’t pass?

A: Yes, if you don’t pass a subject test, you have the opportunity to retake that specific test. There are usually waiting periods and restrictions on the number of retakes allowed, so it’s essential to review the policies set by your local GED testing center.

Q: How long is the GED credential valid?

A: The GED credential does not expire. Once you earn your GED, it is considered a lifelong certification of your high school equivalency.

GED – All About GED – What GED is? For Whom GED is?

All About GED – What GED is?

The GED Test, or General Educational Development Test, is an internationally recognized high school equivalency exam. It is designed for individuals who did not complete their traditional high school education and provides them with an opportunity to earn a credential that is equivalent to a high school diploma.

GED Test, A Comprehensive Exam

The GED Test, commonly known as the General Educational Development Test, is a comprehensive examination that offers individuals an alternative path to attaining a high school equivalency credential.

Specifically designed for those who were unable to complete their traditional high school education, the GED Test provides a valuable opportunity to earn a diploma equivalent to a high school diploma.

With its international recognition, the GED Test serves as a viable option for individuals seeking to further their education, enhance their career prospects, or pursue higher education. By successfully passing the GED Test, individuals can open doors to a variety of opportunities, including better job prospects, access to higher education institutions, and personal fulfillment.

A Brief History of the GED

The General Educational Development (GED) Test has a rich history that spans several decades. From its inception to its current form, the GED has served as a pathway for individuals to obtain a high school equivalency credential. This article provides a concise overview of the key milestones in the history of the GED.

Development of the GED Test:

In the late 1930s, during the Great Depression, the American Council on Education (ACE) introduced the GED Test as a means to assess the academic skills and knowledge of individuals who had not completed high school. The test aimed to create opportunities for those who were unable to pursue traditional education due to economic challenges or other circumstances.

Over time, the GED Test evolved and adapted to meet changing educational standards and societal needs.

Expansion and Standardization:

In the 1940s and 1950s, the GED Test gained recognition and expanded beyond its initial purpose. Colleges, employers, and the military widely accepted the test as a valid alternative to a high school diploma. They undertook efforts to standardize the test, ensuring consistency and fairness in evaluating the abilities of test takers across different regions.

However, advancements in education and technology prompted further updates to the GED Test.

Modernization and Computerization:

In the late 20th century, the GED Test underwent significant modernization efforts. In 1988, the test introduced a computer-based version, allowing for more efficient administration and faster results. This shift to computerization facilitated the integration of multimedia elements, adaptive testing, and enhanced test security measures.

In recent years, the GED Test has continued to evolve to meet the demands of a changing educational landscape.

Alignment with Common Core Standards:

In 2014, the GED Testing Service aligned the exam with the Common Core State Standards, a set of educational benchmarks aimed at ensuring consistent and rigorous learning outcomes. This alignment aimed to enhance the relevance and value of the GED credential, preparing test takers for college and career success.

Today, the GED Test remains an essential pathway for individuals seeking educational and career opportunities.

Eligibility Requirements:

To take the GED Test, individuals must meet certain eligibility requirements. Those requirements ensure that individuals who can benefit from obtaining a high school equivalency credential take the test.

To be eligible for the GED Test, prospective test takers must typically be at least 16 years old, although specific age requirements may vary by jurisdiction.

Additionally, Candidates who did not complete high school, or have graduation or euivalent diploma and wish to obtain an equivalent credential can appear in the GED test.

However, individuals who did not complete high school and are seeking an alternative path to obtain a recognized credential can take advantage of the GED test.

By meeting the eligibility criteria, individuals can embark on the journey of earning their GED credential and unlocking a range of educational and career opportunities.

GED Tests:

The General Educational Development is a series of five tests provides people who have not completed high school, tests covering the different areas of knowledge a student must be competent with in order to graduate from high school.

The Five tests are:

Reasoning Through Language Arts (RLA):

The Reasoning Through Language Arts test assesses the ability of test takers to read and comprehend written passages, analyze and evaluate arguments, and demonstrate effective writing skills. This test focuses on critical thinking, reading comprehension, and written communication.

Mathematical Reasoning:

The Mathematical Reasoning test evaluates the mathematical knowledge and skills of test takers. It covers a wide range of topics, including algebra, geometry, statistics, and data analysis. The test assesses problem-solving abilities and mathematical reasoning through both multiple-choice and constructed response questions.

Social Studies:

The Social Studies test examines the knowledge and understanding of various social science subjects, such as history, geography, civics, and economics. Candidates should analyze primary and secondary sources, interpret historical events, and demonstrate a grasp of key concepts in social studies.

Science:

The Science test evaluates the understanding of scientific concepts and principles, as well as the ability to analyze scientific data and draw conclusions. It covers topics from various scientific disciplines, including biology, chemistry, physics, and Earth science. The test assesses critical thinking, scientific inquiry, and data interpretation skills.

Civics:

The Civics test focuses on assessing the knowledge and understanding of the U.S. government, constitution, and democratic principles. Candidates needs to demonstrate knowledge regarding the rights and responsibilities of citizens, the structure of government, and the political process.The Civics test aims to promote civic literacy and engagement among test takers.

Writing Skills (75 minute multiple-choice and 45 minute essay):
Social Studies (70 minutes)
Science (80 minutes)
Literature (65 minutes)
Mathematics (90 minutes)

Conclusion:

The GED Test has a storied history, providing countless individuals with a second chance to earn a high school equivalency credential. From its early origins to its current form, the GED Test has adapted and modernized to meet the evolving needs of test takers and the educational landscape. As it continues to serve as a recognized alternative to a high school diploma, the GED Test empowers individuals to pursue higher education, secure employment, and achieve their personal goals.

Online classes Pakistani Tutors

September 8, 2020Online Classes by Pakistani Tutors, Online Tuition Pakistan, Online Tuition Saudi Arabia, Online Tutor Pakistan, Online Tutor Saudi Arabia, Pakistani Tutorsacademy, Foundation Classes for Kids, math, math skills, math tutor, online academy, online tuition, online tuition in Karachi, Online Tuition Pakistan, Online Tuition Saudi Arabia, online tuitions, online tutor, online tutor in Karachi, online tutor Pakistan, Online Tutor Saudi Arabia, online tutoring, online tutors, pakistan online, tuition, tuition pakistan, tuitions, tutor, tutor pakistan, tutor pakistanonline, tutorsalsaudia

Online classes Pakistani Tutors

Online Classes for Junior Students

Experience the power of Online Pakistani Tuition at Al-Saudia Virtual Academy, Pakistan’s first and largest online tuition academy.

Our expert Pakistani tutors are dedicated to building a strong foundation for your child’s academic success. Join us to eliminate the hurdles of studies and provide your child with the attention they need to thrive.

Also, Our foundation building classes cater to students who may not be performing well in their schools and require regular check-ins for their online work and assignments.

We understand that parents in Western countries like the USA, Canada, Australia, and the UK may have busy schedules and find it challenging to monitor their child’s academic progress and assist with assignments.

Let us bridge that gap and guide your child towards a brighter future through our comprehensive Online Pakistani Tuition program.

Best and Expert Pakistani tutor:

Get the best Pakistani tutor! Our experienced tutors have decades of teaching expertise, focusing on challenging subjects like math, geometry, and algebra, tailored to meet every student’s needs.

Special math Classes for Kids

Looking for Math tutors for kids? Our special math tutoring program is designed to make algebra and other math concepts easier to understand for children in their earlier stages of learning. Our worksheets emphasize mental math techniques, which not only help boost students’ confidence in problem-solving but also equip them with valuable skills for their academic journey.

Moreover, The positive feedback from parents who have witnessed the transformation in their children’s education brings us immense satisfaction. Our students are excelling in their marks and becoming actively engaged in their class activities.

Furthermore, At Al-Saudia, we strive to be an institute of trust, continuously seeking ways to enhance our foundation programs. We hire professionals to make our programs more powerful and effective. Additionally, Your valuable suggestions and feedback are crucial to our improvement, and we welcome you to share them with us via email at info@pakistanonlinetuition.com. Thank you for your support!

Join Al-Saudia Virtual Academy

Al-Saudia Virtual Academy, your ultimate destination for online tuition in Pakistan. We take pride in being one of the largest, most reliable, and trusted tutoring academies operating worldwide. With a strong commitment to academic excellence, we offer online tutoring services that cater to students from all corners of the globe.

Expert Online Classes By Pakistani Tutors

We reach students in Saudi Arabia (Riyadh, Dammam), Kuwait, Qatar (Doha), Bahrain, and the UAE (Dubai, Abu Dhabi). However, we don’t stop there; our tutoring services cover almost every English-speaking country worldwide.

At Al-Saudia Virtual Academy, we prioritize delivering high-quality education to our students. Our dedicated tutors provide personalized attention, empowering each student to reach their full potential.

Whether your child needs help in Math, Science, English, or any other subject, we offers a flexible and convenient solution. We are committed to fostering a love for learning and academic success among our students.

Join us at Al-Saudia Virtual Academy, where knowledge knows no bounds, and education transcends geographical barriers. Together, let’s embark on a journey of learning and growth.

Mathematics Worksheets

September 8, 2020Mathematics Education, Online mathematics Tuition Pakistan, Online Tuition Pakistan, Online Tuition Saudi Arabia, Online Tutor Pakistan, Online Tutor Saudi ArabiaBasic Arithmetic, Homework Help, Integration Notes, Integration Worksheet, math, Math Exercises, Math Practice, Math Resources, math skills, math tutor, Math Worksheets, online tutor, online tutor Pakistan, Online Tutor Saudi Arabia, Printable Worksheets, Problem Solving, statistics, Stats Tutor, Trigonometry Tutoralsaudia

Integration Made Easy

By Masood Amir

Mathematics Worksheets, ASVA provide calculus and Algebra worksheets.

Calculus:

To measure change or variation of a function with respect to the independent variable we use Calculus.

Differential Calculus: (Mathematics Worksheets)

Differrential Calculus used to measure change or variation of a function in a very small invterval of time.

Integral Calculus:

The branch of calculus used to measure changes or variation over an interval of independent variable, called Integral calculus, e.g to find length of curve, the area of region and the volume of a solid in a specified period of time.

The technique used to measure such changes or variation called “Integration” or “Antiderivatives”. It a reverse process of differentiation.

Mathematically, Integration defined as “ If $f'(x)$ represents the differential coefficient of $f(x)$ , we need to find $f(x)$ , if we have $f'(x)$ or $dy/dx$ .

Integration

Notation: $''∫''$ used to show the integration, it is a symbol of $``S''$ derived from the word $``Sum''$ . i.e. Integration is a process in which we have to sum up the derivatives over a specified interval and to find the function.

Techniques of Integration:

As we know that integration is the reverse process of differentiation, our problem is to find the function $f(x)$ or $Y$ , when $f'(X)$ or $dy/dx$ is given.

$dy/dx &= f'(X)$

$∫dy &= ∫f '(X)dx$

$Y &= f(x)$ is our solution

Ist Formula of Integration (1st Rule of Integration)

Indefinite Integration:

Ist Formula of Integration (Ist Rule of Integration):

Let

$\int dy = \int x^n dx$

$y = \frac{x^{n+1}}{n+1} + C$

Why $``C''$ :

In the process of differentiation, we eliminate constant, as the derivative of a constant is “ $zero$ “.

So, In functions like $x^n$ , $x^n + 6$ , $x^n - 3$ , $x^n + k$ the derivatives of all of them is $X^{n-1}$ , in finding the anti derivative of $X^{n-1}$ , we put a constant “ $C$ ”, as we don’t know which constant was present in the original function, and can be found If we have initial boundary values (Definite Integral).

Example: Solve $\int x^n \, dx$

Solution:

$\int dy = \int x^3 dx$

$y = \frac{x^{3+1}}{3+1} + C$

$y = \frac{x^{4}}{4} + C$

Example: Solve

$\int (x^3 + x^2 + 5x + 6) \, dx$

Solution:

$\int (x^3 + x^2 + 5x + 6) \, dx$

$\int x^3 \, dx + \int x^2 \, dx + \int 5x \, dx + \int 6 \, dx$

$\frac{x^4}{4} + \frac{x^3}{3} + \frac{5x^2}{2} + 6x + C$

Worksheet # 1

Find the Integral of the following:

SET 1

(1) $\begin{align*} 1. & \quad \int (x^3 - 4x^2 + 5x - 6) \, dx \\ 2. & \quad \int (3x^5 - 4x^3 + 3x^2) \, dx \\ 3. & \quad \int (ax^5 - bx^4) \, dx \\ 4. & \quad \int \left( \frac{x^3}{2} - \frac{5x^4}{3} + 3x^2 \right) \, dx \\ 5. & \quad \int (4\sqrt{3}x^2 - 2x) \, dx \\ 6. & \quad \int \left( 3x + 5x^2 - \frac{x^3}{2} - 0.4x^4 \right) \, dx \\ 7. & \quad \int \left( x(8x - \frac{1}{2}) \right) \, dx \\ 8. & \quad \int (2 - x)(4 + 3x) \, dx \\ 9. & \quad \int \left( x^{-3} + x^{-4} \right) \, dx \\ 10. & \quad \int \left( (2x^3 - 3)(3x^4) \right) \, dx \\ 11. & \quad \int \left( 4x^7 + 3x^{12} - 5x^8 + 2x - 1 \right) \, dx \\ 12. & \quad \int \left( ax^3 - bx^2 + cx - d \right) \, dx \\ 13. & \quad \int \left( \frac{1}{x^3} + \frac{2}{x^2} - 6 \right) \, dx \\ 14. & \quad \int \left( -3x - 8 + 2\sqrt{x} \right) \, dx \\ 15. & \quad \int \left( (x^3 - 5)(2x + 5) \right) \, dx \\ 16. & \quad \int \left( 7x - 6 + 5\sqrt{x} \right) \, dx \end{align*}$

Online Tuition

Tuition Pakistan

Online Tutor Pakistan

Al-Saudia Virtual Academy

Mathematics Notes

September 8, 2020Mathematics Notes, Online Tutor Pakistan, Online Tutor Saudi Arabiamath, math tutor, Online Tuition Saudi Arabia, online tutor, online tutor Pakistan, Online Tutor Saudi Arabia, Pakistani Tutors, statistics, Stats Tutor, Trigonometry Tutoralsaudia

Mathematics Notes

Call Us: +92-332-3343253

Skype Id: ascc576

Email at: info@pakistanonlinetuition.com

Mathematics Notes: Optimized for Effective Learning

Comprehensive Calculus Notes:

Our online Mathematics notes offer a comprehensive coverage of Calculus, ensuring a deep understanding of concepts like derivatives, integrals, and limits. These notes facilitate active learning and foster problem-solving skills.

Statistical Insights:

Our online Statistics notes equip students with the knowledge needed to analyze and interpret data effectively.

.Component and Defination of Mathematical Terms:

1.Sets
2.Complex Numbers
3.Quadratic Equations
3.Systems of Two Equations
4.Matrices

Determinants and Inverse Matrices

Groups

Sequence and Series

Permutations and Combinations

Introduction to Probability

Mathematical Induction

The Binomial Theorem

Fundamental Trigonometry

Trigonometric Identities

Trigonometric Functions

Solutions of Triangles

Inverse Trigonometric Functions

and Trigonometric equations

Orthogonal Trajectory

SETS

A set is a well-defined collection of distinct objects, considered as an object in its own right. The objects in a set are called elements or members of the set. Sets usually denote by capital letters, and we list their elements within curly braces, like this: A = {1, 2, 3, 4}.

Definition:

A set is a collection of distinct elements, typically written as: where are the elements of the set . If an element belongs to a set, we say it is a member of the set, and this is denoted by if $x$ is an element of $A$ .

Types of Sets:

Finite Set: A set with a limited number of elements.
Example:
Infinite Set: A set with an unlimited number of elements.
Example:
Subset: A set where all elements of one set are contained in another.
Example:
Universal Set: The set that contains all objects under consideration, usually denoted by .
Empty Set (Null Set): A set that contains no elements, denoted by
Example:
Power Set: The set of all subsets of a set, including the empty set and the set itself.
Example: Power set of is
Equal Sets: Two sets are equal if they have exactly the same elements.
Example:
Union of Sets: The set containing all elements from both sets. A={1,2,3) & B={2,4,6)
Example:
Intersection of Sets: The set containing only elements common to both sets.
Example:

Applications of Sets:

Engineering:

Sets are crucial in computer science, particularly in the development of algorithms, data structures, and databases. Engineers also use sets to model systems, solve optimization problems, and perform operations like union and intersection for network analysis and circuit design.

Mathematics:

In mathematics, sets form the foundation for various concepts such as probability, calculus, and geometry. Set theory is used in solving complex problems, formulating proofs, and understanding functions.

Economics:

Sets help in analyzing data, consumer behavior, and market segmentation. Economists use sets to categorize and analyze different populations and to study the overlap and intersection of markets.

Physics:

In physics, sets are applied in quantum mechanics and relativity theory. Sets describe physical quantities, particle systems, and the union of various physical states.

Computer Science:

In programming, sets are used to manage collections of data, solve problems related to databases, and execute operations such as searching, sorting, and filtering.

Got Top

Complex Numbers:

Definition, Operations, and Applications

Complex numbers extend the concept of real numbers to include solutions to equations that do not have real solutions, such as the square root of negative numbers. They are essential in various fields of mathematics and engineering.

Definition

A complex number is a number of the form:

$z = a + bi$

where:

$a$ is the real part of the complex number,
$b$ is the imaginary part,
$i$ is the imaginary unit, defined as $i = \sqrt{-1}$ .

For example, in the complex number $3 + 4i$ , $3$ is the real part and $4$ is the imaginary part.

Basic Operations

1. Addition: To add two complex numbers, add their real parts and imaginary parts separately.

$(a + bi) + (c + di) = (a + c) + (b + d)i$

2. Subtraction: To subtract two complex numbers, subtract their real parts and imaginary parts separately.

$(a + bi) - (c + di) = (a - c) + (b - d)i$

3. Multiplication: To multiply two complex numbers, use the distributive property and apply the fact that $i^2 = -1$ .

$(a + bi)(c + di) = (ac - bd) + (ad + bc)i$

4. Division: To divide two complex numbers, multiply the numerator and the denominator by the conjugate of the denominator.

$\frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{c^2 + d^2} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2}$

5. Conjugate: The conjugate of a complex number $a + bi$ is $a - bi$ . Conjugates are useful in division and finding magnitudes.

$Conjugate of (a + bi) = a - bi$

6. Magnitude: The magnitude (or modulus) of a complex number $a + bi$ is given by:

$|a + bi| = \sqrt{a^2 + b^2}$

7. Argument: The argument (or angle) of a complex number $a + bi$ is the angle $\theta$ such that:

$\theta = \tan^{-1}\left(\frac{b}{a}\right)$

Polar Form of Complex Numbers

A complex number can be represented in the form

$z = a + bi$

, where $a$ is the real part of the complex number,
$b$ is the imaginary part,
$i$ is the imaginary unit, defined as $i = \sqrt{-1}$ .

A complex number $z$ can be expressed in polar form as:

$z = r \left( \cos \theta + i \sin \theta \right)$

where $r$ is the magnitude (or modulus) of the complex number, given by

$r = |z| = \sqrt{x^2 + y^2}$

and $\theta$ is the argument (or angle) of the complex number, measured from the positive $x$ -axis, given by

$\theta = \arg(z) = \tan^{-1} \left( \frac{y}{x} \right)$

Euler’s Form of Complex Numbers

Euler’s formula relates complex exponentials to trigonometric functions:

Alternatively, the polar form can also be written using Euler’s formula as:

$z = r e^{i \theta}$

This is a more compact and elegant way of expressing the polar form. Here,

$e^{i \theta}$

represents the complex exponential, and $\theta$ is the argument of the complex number. This form is particularly useful for multiplication, division, and finding powers and roots of complex numbers.

Examples 1:

Convert

$z = 3 + 4i$

into Polar & Euler’s For

To convert into polar form:

Magnitude:

$r = \sqrt{3^2 + 4^2} = 5$

The argument $\theta$ is:

$\theta = \tan^{-1}\left(\frac{4}{3}\right) \approx 53.13^\circ$

Thus, the polar form is:

$z = 5 \left(\cos{53.13^\circ} + i \sin{53.13^\circ}\right)$

In Euler’s form:

$z = 5 e^{i 53.13^\circ}$

Examples 2:

Convert

$z = -1 + i$

into Polar & Euler’s For

To convert into polar form:

Magnitude:

$r = \sqrt{-1^2 + 1^2} = \sqrt{2}$

Argument:

$\theta = \tan^{-1}(1 / -1) = 135^\circ \, \text{or} \, \pi=\ - \frac{\pi}{4}$

Polar form:

$z = \sqrt{2} (\cos{135^\circ} + i \sin{135^\circ})$

Euler’s Form

$z = \sqrt{2} e^{i 135^\circ}$

Derivation of Euler’s Form:

Euler’s form of a complex number provides a powerful and elegant way to represent complex numbers using exponential functions. Here’s a step-by-step explanation of Euler’s form and how it is derived from the polar form using the expansions of cosine and sine.

Euler’s Form of a Complex Number

Euler’s form of a complex number $z$ is given by:

$z = r e^{i \theta}$

where:

$r$ is the magnitude of the complex number.
$\theta$ is the argument (angle) of the complex number.
$e^{i\theta}$ is the exponential function involving the imaginary unit $i$ .

Derivation from Polar Form

Start with the Polar Form:The polar form of a complex number $z$ is expressed as:

$z=r(cos⁡θ+isin⁡θ)$

where:

- $r$ is the magnitude of the complex number.
- $\theta$ is the argument or angle.

Use Euler’s Formula:Euler’s formula states that:

$z = cos⁡θ+isin⁡θ$

is equal

$z = e^{i\theta}$

This is a fundamental result in complex analysis and connects exponential functions with trigonometric functions.

Substitute Euler’s Formula into the Polar Form:

To express the polar form in terms of Euler’s formula, substitute Euler’s formula into the polar form expression:

$z=r(cos⁡θ+isin⁡θ)$

can be written as:

$z = r e^{i\theta}$

This substitution uses the fact that

$e^{i\theta}$

can be expanded as

$cos{\theta} + i \sin{\theta}$

Expansion of Cosine and Sine

To see this more clearly, let’s expand

$e^{i\theta}$

using its Taylor series:

- Taylor Series for $e^{i\theta}$
  :

$e^{i\theta} = \sum_{n=0}^{\infty} \frac{(i\theta)^n}{n!}$

Expanding

$(i\theta)^n$

$i^n\theta^n$

So:

$e^{i\theta} = \sum_{n=0}^{\infty} \frac{i^n\theta^n}{n!}$

Separate Real and Imaginary Parts:

To separate the real and imaginary parts, recall that:

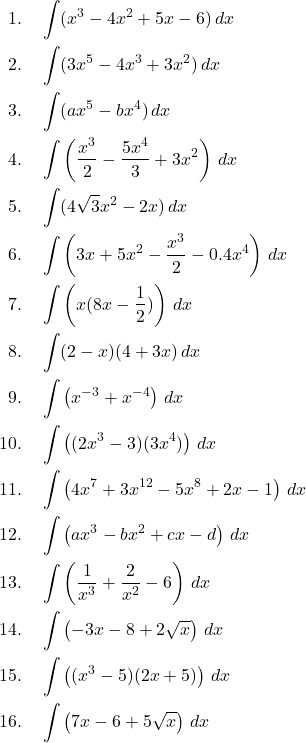
$i^n = \begin{cases} 1 \quad \text{if } n \mod 4 = 0 \\ i \quad \text{if } n \mod 4 = 1 \\ -1 \quad \text{if } n \mod 4 = 2 \\ -i \quad \text{if } n \mod 4 = 3 \end{cases}$

Grouping terms:

Real Part:

$\text{Re}(e^{i\theta}) = \sum_{\text{n even}} \frac{(-1)^{n/2} \theta^n}{n!} = \cos{\theta}$

Imaginary Part:

$\text{Im}(e^{i\theta}) = \sum_{\text{n odd}} \frac{(-1)^{(n-1)/2} \theta^n}{n!} = \sin{\theta}$

Hence, combining these:

$e^{i\theta} = \cos{\theta} + i \sin{\theta}$

WorkSheets On Complex Number

Convert Cartesian form into Polar & Euler’s Form

Convert $z = 2 + 3i$ into polar form.
Convert $z=−4+5i$ into Euler’s form.
Find the polar form of $z=5+12i$ .
Convert $z=−6+8i$ to Euler’s form.
Express $z=1+i$ in polar form.
Find the Euler’s form of $z=−3+4i$ .
Convert $z=−2−3i$ into polar form.
Convert $z=7−5i$ to Euler’s form.
Express $z=8+6i$ in polar form.
Find the polar form of $z=9+7i$ .
Convert $z=−3+3i$ to Euler’s form.
Express $z=4−4i$ in polar form.
Find the polar form of $z=−5−2i$ .
Convert $z=6+2i$ into Euler’s form.
Express $z=−2+6i$ in polar form.

Convert Polar & Euler’s form into Cartesian Form

$z = 4(\cos 30^\circ + i \sin 30^\circ)$ , convert to Cartesian form.
Convert $z = 6e^{i\frac{\pi}{6}}$ into Cartesian form.
Convert $z = 5(\cos 60^\circ + i \sin 60^\circ)$ to Cartesian form.
Convert $z = 7e^{i\frac{\pi}{4}}$ to Cartesian form.
Convert $z = 3(\cos 45^\circ + i \sin 45^\circ)$ to Cartesian form.
Convert $z = 2e^{i\frac{\pi}{3}}$ to Cartesian form.
Convert $z = 8(\cos 90^\circ + i \sin 90^\circ)$ to Cartesian form.
Convert $z = 10e^{i\frac{\pi}{2}}$ to Cartesian form.
Convert $z = 12(\cos 135^\circ + i \sin 135^\circ)$ to Cartesian form.
Convert $z = 4e^{i\frac{\pi}{4}}$ to Cartesian form.
Convert $z = 9(\cos 120^\circ + i \sin 120^\circ)$ to Cartesian form.
Convert $z = 5e^{i\frac{\pi}{3}}$ to Cartesian form.
Convert $z = 6(\cos 150^\circ + i \sin 150^\circ)$ to Cartesian form.
Convert $z = 7e^{i\frac{5\pi}{6}}$ to Cartesian form.
Convert $z = 8(\cos 180^\circ + i \sin 180^\circ)$ to Cartesian form.

Applications

1. Engineering:

Complex numbers are used in electrical engineering to analyze AC circuits, where they represent impedance and phase relationships. They simplify the analysis of alternating current (AC) signals and circuits.

2. Control Systems:

In control theory, complex numbers are used to describe system dynamics and stability. The poles and zeros of transfer functions are complex numbers that help in designing and analyzing control systems.

3. Signal Processing:

Complex numbers are employed in signal processing to handle frequency domain analysis. Fourier transforms and filters often use complex numbers to analyze and manipulate signals.

4. Physics:

Complex numbers are essential in quantum mechanics, where they describe wave functions and probability amplitudes. The Schrödinger equation, a fundamental equation in quantum mechanics, uses complex numbers.

5. Mathematics:

Complex numbers are used in various branches of mathematics, including complex analysis, which studies functions of complex variables. They also appear in solutions to polynomial equations and many areas of applied mathematics.

6. Computer Graphics:

In computer graphics, complex numbers are used for transformations and rotations. They help in manipulating images and performing geometric transformations efficiently.

Complex numbers provide a powerful framework for solving problems that cannot be addressed with real numbers alone, making them an indispensable tool in mathematics and engineering.

Got Top
.

Introduction to Quadratic Equations

A quadratic equation is a second-degree polynomial equation in a single variable $x$ , with the general form:

$ax^2 + bx + c = 0$ where $a$ , $b$ , and $c$ are constants, and $a \neq 0$ . The term “quadratic” comes from “quad,” meaning square, since the highest exponent of the variable is $2$ .

Uses and Applications of Quadratic Equations

Quadratic equations are used in various fields, including:

Physics: To describe projectile motion, the trajectory of an object can be modeled using quadratic equations.

Engineering: In structural engineering, quadratic equations help calculate loads, tensions, and forces.

Economics: They are used in cost, profit, and revenue functions, particularly in finding maximum or minimum values.

Biology: Quadratic equations help model population growth, the spread of diseases, or other natural phenomena.
Geometry: These equations are used in determining areas, and for working with parabolas and ellipses.

Quadratic Expressions and Quadratic Equations

Method of Solving Quadratic Expressions $ax^2+bx+c$ , $a \neq 0$

1.Factorisation Method:

The goal is to express the quadratic expression in the form of two binomials:

$ax^2 + bx + c = (px + q)(rx + s)$

where $p, q, r,$ and $s$ are constants, and the equation is solved by finding appropriate factors of $a \times c$ .

2. Completing the Square Method:

To solve the quadratic expression, we can complete the square as follows:

$ax^2 + bx + c = a\left( x^2 + \frac{b}{a}x \right) + c$

The next step is to add and subtract a term to make a perfect square trinomial:

$x^2 + \frac{b}{a}x + \left( \frac{b}{2a} \right)^2 - \left( \frac{b}{2a} \right)^2$

After simplifying, we can rewrite it as:

$\left( x + \frac{b}{2a} \right)^2 - \text{constant}$

3. Quadratic Formula:

The quadratic formula is:

$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

This method can be used for any quadratic equation to find its roots directly.

Factorisation Based on the Value of $a$ and the Sign of $c$

In solving quadratic equations, it is important to consider the value of $a$ and the sign of $c$ .

CASE 1:

If $a = 1$ , we check the sign of $c$ .

If $c$ is positive, both factors have the same sign as $b$ , and their sum equals $b$ .

Example:

$x^2 + 7x + 12 = 0$

First, find factors of $12$ :

$(1, 12), (2, 6), (3, 4)$

Since $3 + 4 = 7$ , we split $7x$ into $3x$ and $4x$ , so the equation becomes:

$x^2 + 3x + 4x + 12 = 0$

Now, factor:

$x(x + 3) + 4(x + 3) = 0$

Thus:

$(x + 3)(x + 4) = 0$

Setting each factor equal to zero:

$x + 3 = 0 \quad \text{or} \quad x + 4 = 0$

So, the solutions are:

$x = -3 \quad \text{and} \quad x = -4$

Similarly we can solve $x^2 - 7x +12 =0$

Case II:

if $c$ is negative, factors subtracted and have different signs, the large factor keep the sign of $b$ .

for example $x^2 - x -12$ , in this case we need to find the factors of $12$ , which when subtracted give us $-1$ , so again the difference of $4$ and $3$ is $1$ , but we put $-$ sign with $4$ nd split $-x$ as $-4x and + 3x$ . now the equation becomes

$x^2 -4x + 3x -12$

$(x -4)(x +3)$

$x-4 =0$ and $x+3=0$

therefore the solution of the above equation are $+4$ and $-3$ .

If $a \neq 0$

we first multiply $a$ and $c$ and the factorize the value of $ac$ , repeat the case I and case II accordingly.

Quadratic Equation Questions

1. Solve the quadratic equation: $x^2 - 4x - 5 = 0$ .
2. Solve the quadratic equation: $2x^2 + 3x - 2 = 0$ .
3. Find the roots of $x^2 - 9 = 0$ .
4. Factor and solve: $x^2 + 6x + 9 = 0$ .
5. Solve for $x$ : $3x^2 - 2x - 8 = 0$ .
6. What are the solutions to $x^2 + 4x + 4 = 0$ ?
7. Solve by completing the square: $x^2 - 6x + 5 = 0$ .
8. Use the quadratic formula to solve: $x^2 - 7x + 10 = 0$ .
9. Solve the equation: $4x^2 - 12x + 9 = 0$ .
10. Solve $x^2 + 8x + 16 = 0$ by factoring.
11. Solve $x^2 - 2x - 3 = 0$ using the quadratic formula.
12. Find the roots of $5x^2 - 20x + 15 = 0$ .
13. Solve $3x^2 + 2x - 8 = 0$ by completing the square.
14. Factor and solve $x^2 - 16 = 0$ .
15. Solve $6x^2 - x - 1 = 0$ using the quadratic formula.
16. Solve for $x$ : $x^2 + 5x + 6 = 0$ .
17. Find the solutions to $x^2 - 25 = 0$ .
18. Solve $7x^2 + 14x + 7 = 0$ by factoring.
19. What are the roots of $9x^2 - 24x + 16 = 0$ ?
20. Solve $2x^2 - 10x + 12 = 0$ using the quadratic formula.

Got Top
.

Methods Of Solving System of Two Linear Equations

solving a system of two linear equations. There are three main methods to solve such systems:

Substitution,
Elimination, and
Graphical Method.
Matrix Method

Substitution Method

Explanation:
In the substitution method, we solve one equation for one variable and substitute that expression into the other equation to find the value of the second variable.

Steps:

Solve one equation for one variable in terms of the other (e.g., solve for
$𝑥 or 𝑦$ .
Substitute the expression into the other equation.
Solve for the second variable.
Use this value to find the first variable.

Example:
Solve the system of equations:

$\begin{align*} x + y &= 7 \quad \text{......(1)} \\ 2x - y &= 4 \quad \text{......(2)}\\ \end{align*}$

Step 1: Solve equation $1$ for $y$ :

$\begin{align*}y &= 7 - x \quad\text{......(3)}\\ \end{align*}$

Step 2: Substitute $y &= 7 - x$ into equation $(2)$

$\begin{align*}2x-(7-x) &= 4\\ \end{align*}$

Step 3: Solve for $x$ :

$\begin{align*}2x-7+x &= 4\\ 3x - 7 &= 4 \\ 3x &= 11 \\ x &= \frac{11}{3} \end{align*}$

Step 4: Put the value of $x$ in eq $(1)$

$\begin{align*}x+y &= 7\\ y+ \frac{11}{3}&=7\\ y &= 7 - \frac{11}{3}\\ y &= \frac{10}{3} \end{align*}$

The solution is:

$\begin{align*}x &= \frac{11}{3}\\ y&=\frac{10}{3}\\ \end{align*}$

Substitution Method: 10 Practice Questions

$\begin{align*} 2x + y &= 5 \quad \text{......(1)} \\ x - y &= 1 \quad \text{......(2)} \end{align*}$

$\begin{align*} x + 3y &= 7 \quad \text{......(1)} \\ 2x - y &= 4 \quad \text{......(2)} \end{align*}$

$\begin{align*} x + y &= 3 \quad \text{......(1)} \\ x - 3y &= 5 \quad \text{......(2)} \end{align*}$

$\begin{align*} x + y &= 3 \quad \text{......(1)} \\ 3x + y &= 9 \quad \text{......(2)} \end{align*}$

$\begin{align*} 4x + y &= 10 \quad \text{......(1)} \\ 2x - y &= 3 \quad \text{......(2)} \end{align*}$

$\begin{align*} x + 2y &= 8 \quad \text{......(1)} \\ 3x - y &= 7 \quad \text{......(2)} \end{align*}$

$\begin{align*} 5x - y &= 11 \quad \text{......(1)} \\ 2x + y &= 4 \quad \text{......(2)} \end{align*}$

$\begin{align*} x + y &= 6 \quad \text{......(1)} \\ 4x - y &= 9 \quad \text{......(2)} \end{align*}$

$\begin{align*} 3x - 2y &= 5 \quad \text{......(1)} \\ x + y &= 4 \quad \text{......(2)} \end{align*}$

$\begin{align*} 2x + 3y &= 12 \quad \text{......(1)} \\ x - y &= 2 \quad \text{......(2)} \end{align*}$

$\begin{align*} 4x - y &= 2 \quad \text{......(1)} \\ x + 2y &= 5 \quad \text{......(2)} \end{align*}$

Continue reading Mathematics Notes →

MA Economics papers

September 8, 2020Online Tuition Pakistan, Online Tuition Saudi Arabia, Online Tutor Pakistan, Online Tutor Saudi Arabia, Pakistani TutorsEco past papers Karachi University, Economics Papers, Economics past paper, Economics tuitions, Economics tutoring, MA Economics Papper, online academy, online Economics tuitions, online Economics tutor, online tuition, Online Tuition Pakistan, online tutor, online tutor Pakistan, Online Tutor Saudi Arabia, Private MA Economics Past Papersalsaudia

MA Economics Past Papers

Call Us: +92332-3343253

Skype id: ascc576

Email: info@pakistanonlinetuition.com

Pakistan Best Online Economics Tuition

Al-Saudia Virtual Academy is Pakistan’s leading online tuition academy, offering the best economics tuitions for students worldwide. Our highly qualified and experienced professors provide top-notch education in the field of economics. With a strong focus on quality, we ensure that students receive comprehensive knowledge and achieve excellent results.

MA Economics Past Paper Assistance

To excel in economics, students need thorough practice and understanding of past papers. Our online economics tutors offer valuable guidance and assistance in solving past papers. By analyzing previous years’ questions, students gain a better understanding of exam patterns and can effectively prepare for their upcoming assessments.

Efficient Economics Tutoring Services

At Al-Saudia Virtual Academy, we provide exceptional online economics tutoring services. Our dedicated tutors utilize effective teaching strategies to help students grasp complex economic concepts. With personalized attention and interactive sessions, students can enhance their understanding of various economic theories and principles.

Online Economics Tutor: A Convenient Learning Option

With the rise of online education, an online economics tutor has become a convenient choice for students worldwide. Our online tutoring platform allows students to access expert economics tutors from the comfort of their homes. This flexibility enables students to schedule sessions according to their convenience, eliminating the need for travel or fixed class timings.

MA Economics Papers: Comprehensive Coverage

We offer comprehensive support for MA economics papers. Our experienced tutors cover various subjects, including microeconomics, public finance, advanced economic statistics, macroeconomics, economics of Islam, mathematical economics, economics of planning, agricultural economics, national income analysis and accounting, and comparative economics. With in-depth knowledge and expertise in these areas, our tutors ensure students have a solid foundation in MA economics.

Pakistan Online Tuition Academy: Trusted Choice

Al-Saudia Virtual Academy is a trusted choice for online tuition in Pakistan. We cater to students from various countries, including the USA, UK, Canada, Saudi Arabia, Kuwait, Qatar, Bahrain, and more. Our tutors are well-versed in different curriculums, specifically those of American states such as Texas, Ohio, Virginia, and Alabama, as well as the UK, Canada, and Australia.

Contact Us for Online Economics Tuition

To avail our online economics tuition services, students can reach out to us through email at info@pakistanonlinetuition.com. Alternatively, they can add our Skype ID: ascc576 or call us at +923323343253. Our dedicated team is available to answer queries, provide information, and assist in arranging tutoring classes, assignment help, and homework support.